Die Gaussche Normalverteilung ist eine eingipflige, symmetrische, glockenförmige Kurve.
Annähern läßt sich die Normalverteilung durch ein Experiment, in dem Sand durch einen Trichter an 2 parallelen Glaswänden vorbei rinnt .
Die Gaussche Normalverteilung wird durch die Formel:
y = a*e-b*x*x
beschrieben .
Ausgesprochen heißt das: y ist gleich a mal e hoch minus b mal x mal x .
x wird zb von – 3 bis 3 variiert . a und b sind festzulegende konstante Werte . e ist die Eulersche Zahl e= 2,7182… . y wird zu jedem x Wert ausgerechnet.
Ein einfaches Beispiel:
Man denke sich einen Querschnitt durch einen Berg. Der Berg ist spiegelsymmetrisch aufgebaut. Der Gipfel des Berges liegt über dem Mittelpunkt . In obiger Formel liegt der Gipfel bei x = 0. Die Breite des Berges und die Steilheit des Berghanges kann sich verändern . Sie wird mittels des b Wertes (oder des Sigmawertes s ) beschrieben . Ist b sehr groß, ist der Berg schmal und steil. Ist b sehr klein , ist der Berg sehr breit. Die Höhe des Berges hängt an dem Faktor a. Je größer der a Wert , desto höher der Berg.
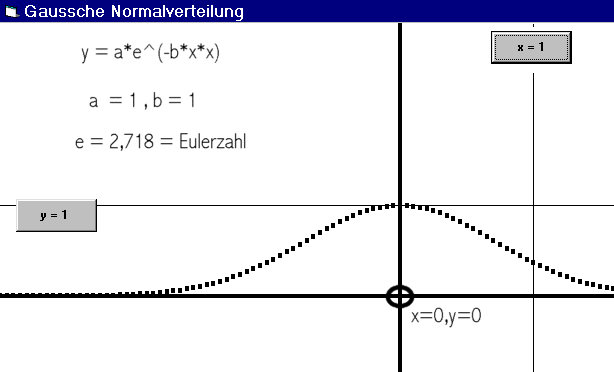
Nehmen sie einfach einmal folgende Werte und fangen sie für verschiedene x Werte zu rechnen an:
- e = 2.718 = Eulersche Zahl
- a = 1: b = 1: beliebig angenommene Werte für a und b
y = a * e ^ (-b * x * x) = 2,718^(-x*x)
Für alle x zwischen – 3 und + 3 sind in der obigen Abbildung die y Werte errechnet und in eine Grafik übertragen worden . Als Hilfslinien wurde die waagrechte Gerade y = 1 und die senkrechte Gerade x = 1 eingezeichnet.
Beispielrechnungen :
x = 0 , dann ist y = 1 ,
- denn -b*x*x = -1*0*0 = 0
- und e hoch 0 = 1 und
- a *e hoch = 1 * 1 = 1
x = 1 , dann ist y = 0,368
- denn es rechnet sich
- Hochzahl: -b * x * x = -1*1*1 = -1
- e hoch – 1 = 1 / e = 1 / 2,718 = 0,368
- y = a * 0,368 = 1 * 0,368 = 0,368
x = 2 , dann ist y = 0,018
- denn es rechnet sich
- Hochzahl: -b * x * x = -1*2*2 = -4
- e hoch – 4 = 1 / e*e*e*e = 1 / 2,718 *2,718*2,718*2,718 = 0,018
- y = a * 0,018 = 1 * 0,018
Man kann auch negative Werte für x einsetzen , durch das Quadrieren von x macht das am Ergebnis für y nichts aus.
Eine Werteübersicht von x = – 3 bis x = 3 in 0.1 Schritten zeigt folgende Tabelle
-3 1,2352501873527E-04
-2,9 2,22824071415957E-04
-2,8 3,93989178289048E-04
-2,7 6,82843991066462E-04
-2,6 1,16004196902112E-03
-2,5 1,93170552746327E-03
-2,4 3,15299407179942E-03
-2,3 5,04452637225929E-03
-2,2 7,91102305913303E-03
-2,1 1,21607375273312E-02
-2 1,83232366388273E-02
-1,9 2,70619742737699E-02
-1,8 3,91770539120532E-02
-1,7 5,55928683823651E-02
-1,6 7,73252622980479E-02
-1,5 0,10542381597419
-1,4 0,140887049243167
-1,3 0,184551859521179
-1,2 0,236963135905068
-1,1 0,298234693001484
-1 0,367917586460632
-,9 0,444895428867152
-,8 0,527327415239601
-,7 0,612657519638419
-,6 0,697702368259124
-,5 0,778820970680916
-,4 0,852157925708685
-,3 0,913939713737006
-,2 0,960793423910691
-,1 0,990050860275653
0 1,0
ab hier werden die Werte symmetrisch zu den negativen x Werten wieder kleiner
,1 0,990050860275654
,2 0,960793423910692
,3 ,913939713737007
,4 ,852157925708686
,5 ,778820970680918
,6 ,697702368259125
,7 ,612657519638421
,8 ,527327415239603
,9 ,444895428867153
1,0 ,367917586460634
1,1 ,298234693001485
1,2 ,236963135905069
1,3 ,18455185952118
1,4 ,140887049243168
1,5 ,105423815974191
1,6 7,73252622980484E-02
1,7 5,55928683823655E-02
1,8 3,91770539120535E-02
1,9 2,70619742737701E-02
2 1,83232366388275E-02
2,1 1,21607375273313E-02
2,2 7,9110230591331E-03
2,3 5,04452637225934E-03
2,4 3,15299407179945E-03
2,5 1,9317055274633E-03
2,6 1,16004196902114E-03
2,7 6,8284399106647E-04
2,8 3,93989178289053E-04
2,9 2,2282407141596E-04
3 1,23525018735272E-04
Diese Werte wurden mit folgendem Visual Basic Programm berechnet:
Sub Befehl1_Click ()
- For x = -5 To 5 Step .1
- y = 2.718 ^ (-x * x)
- t = t & x & “ “ & y & Chr(13) & Chr(10)
- Next x
- text1.Text = t
End Sub
Das entsprechende Gambas Programm lautet:
PUBLIC SUB Form_Open()
DIM x AS Float
DIM y AS Float
DIM t AS String
FOR x = -5 TO 5 STEP 0.1
- y = 2.718 ^ (-x * x)
- t = t & Str(x) & “ “ & Str(y) & Chr(13) & Chr(10)
NEXT
PRINT t
END
Wie schaut die Grafik bei verschiedenen a – Werten aus ?
Der Gipfel wird höher , die Wendepunkte am Hang bleiben aber unverändert bei denselben x – Werten , dh der Berg wird nicht breiter.
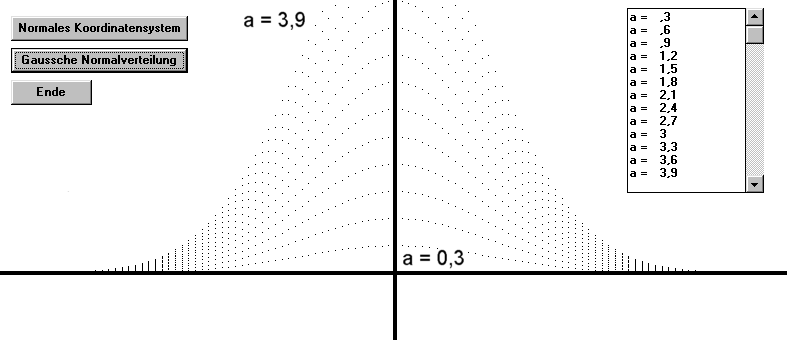
Wie schaut die Grafik bei verschiedenen b – Werten aus ?
Der Gipfel bleibt gleich hoch , der Berg wird aber immer breiter je kleiner der b- Wert wird.
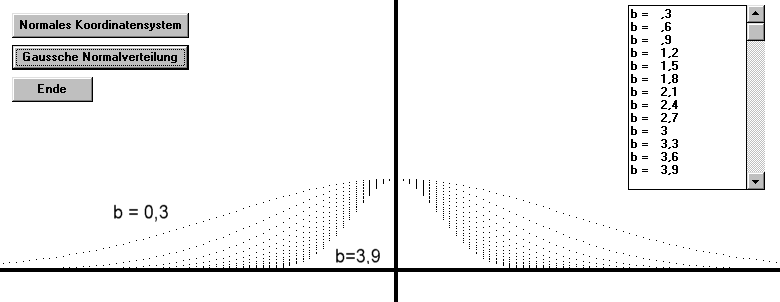
Interessant wird es , wenn man für b einen negativen Wert eingibt.
y = a * e ^ (-b * x * x)
Dann dreht sich die Kurve nach oben um und hat keine Wendepunkte mehr.
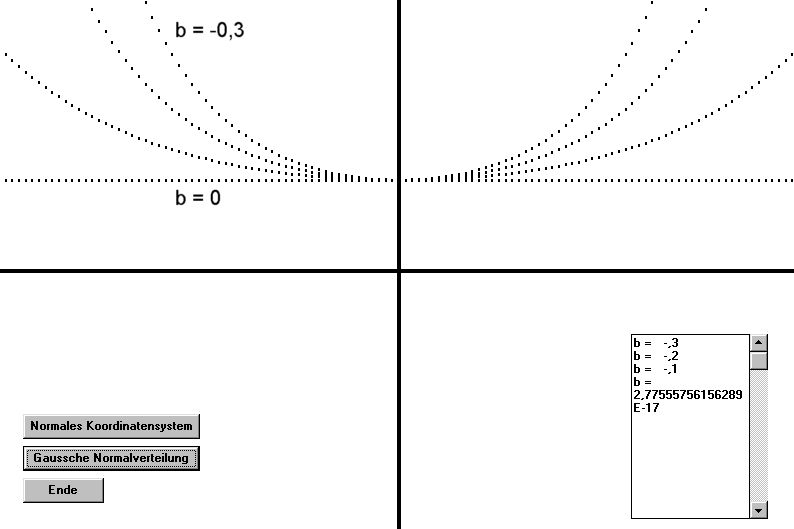
Für b = 0 erhält man logischerweise eine Gerade mit der Formel y = 1 für alle Wert von x .
Bei negativen a Werten gibt es keine Probleme , sondern die Gaussche Normalverteilung wird nur nach unten ins negative gespiegelt. Spiegelungsachse ist die Gerade x = 0, also die x – Achse.
Verschiebung des Berges entlang der x Achse
Will man den Gipfel der Normalverteilung entlang der x Achse verschieben , so muß man einen neuen Parameter einführen, der die Verschiebung vom Nullpunkt angiebt. Dieser Faktor wird meist m genannt.
Statt x setzt man dann in die Formel y = ae-b*x*x den Wert x-m ein:
y = ae-b*(x-m)*(x-m)
Man kann die Formel auch anders formulieren , wenn man die Standardabweichung in die Formel integriert haben will. Außerdem kann man den Maximalwert noch entlang der x Achse verschieben.
( m = x mittel = x mit Querbalken darüber) . Die Breite des Berges und die Steilheit wird dann mittels des des Sigmawertes s beschrieben . Ist Sigma sehr groß, ist der Berg sehr breit. Ist Sigma klein ist der Berg schmal und steil.
Sauber ausformuliert finden sich hinter den Konstanten a und b dann folgende Werte:
a = 1/ (Sigma * ( 2 * Pi )^0.5 )
b = 1/(2*Sigma*Sigma)
allgemeiner kann man die Kurve auch so formulieren:
Sie hat ihre Wendepunkte bei x Mittel – sigma und x Mittel + sigma
(siehe auch Standardabweichung)
Ihr kommt in der Statistik eine besondere Bedeutung zu, da viele Methoden von dieser Verteilungsform ausgehen.
Bei realen Datensätzen mit geringen Fallzahlen ist sie aber eher selten und tritt meist nur angenähert auf:
Nach dem zentralen Grenzwertsatz sind Zufallsvariablen besser an die Normalverteilung angenähert, je größer ihre Anzahl ist.
(Nach Sachs; Angewandte Statistik: „Die zentrale Bedeutung der Normalverteilung besteht darin, daß eine Summe von vielen unabhängigen, beliebig verteilten Zufallsvariablen gleicher Größenordnung angenähert normalverteilt sind.)
Deshalb ist es wichtig, seine Daten vor der Analyse auf Normalverteilung zu prüfen und darauf aufbauend die richtige Statistik zu benutzen
Normalverteilung
Gaußsche Normalverteilung, eine in der Inferenzstatistik besonders wichtige stetige theoretische Verteilung, hergeleitet von C. F. Gauß. –
1. Die expliziten Parameter der Normalverteilung sind der Erwartungswert m ( Mittelwert) und die Varianz s2 . Mit Hilfe der Standardtransformation können Normalverteilungen mit beliebiger Parameterlage in die
- Standardnormalverteilung (m = 0; s2 = 1)
überführt werden. Für die Auswertung der Dichtefunktion bzw. Verteilungsfunktion der Standardnormalverteilung existieren Tabellenwerke, in denen Wahrscheinlichkeitsdichten bzw. Werte der Verteilungsfunktion verzeichnet sind. Die Tabellen der Standard-Normalverteilung können daher zur Auswertung beliebiger Normalverteilungen herangezogen werden. –
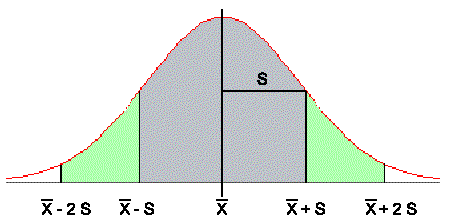
2. Eigenschaften: Bei graphischer Darstellung ergibt die Dichtefunktion einer Normalverteilung eine glockenförmige Kurve, die symmetrisch zur Geraden x = m ist. Der Erwartungswert m fällt mit dem Modus und dem Median zusammen. Die Glockenkurve hat Wendepunkte bei den Abszissen m + s bzw. m – s. Für eine m-normalverteilte Zufallsvariable X gilt (gerundete Werte):
W{m – s < X < m + s} = 0,6827 d.h ca 0,7 aller Werte liegen innerhalb dieser Grenzen
W{m – 2 s < X < m +2 s} = 0,9545 d.h ca 95 % aller Werte liegen innerhalb der 2s Grenzen
W{m – 3 s < X < m +3 s} = 0,9973
3. Bedeutung: Annähernd normalverteilte Merkmale sind in der Wirtschaft gelegentlich, im technisch-naturwissenschaftlichen Bereich des öfteren zu beobachten. Dies ist durch den Zentralen Grenzwertsatz begründbar. Außerdem ist z. B. der Stichprobendurchschnitt (arithmetisches Mittel) bei großem Stichprobenumfang annähernd auch dann als normalverteilt zu betrachten, wenn über die Verteilung der Grundgesamtheit nichts bekannt ist. Schließlich eignet sich die N. zur Approximation vieler theoretischer Verteilungen unter gewissen Voraussetzungen, etwa der Binomialverteilung, der hypergeometrischen Verteilung oder der Chi-Quadrat-Verteilung.
Normalverteilung
Die GAUß- oder Normalverteilung wird häufig angewendet, um die Lage und die Streuung von Meßwerten zu beschreiben.
Jede Normalverteilung hat folgende Eigenschaften:
- eingipflig
- stetig mit Werten zwischen + Unendlich und – Unendlich , d.h. alle Werte die angenommen werden können, entstammen der Menge der reellen Zahlen
- symmetrisch
- nähert sich asymptotisch der x Achse (Asymptote = Näherungslinie)
- ist durch den Mittelwert m und die Streuung gekennzeichnet. Die Streuung kann als Standardabweichung s (sprich „sigma“) oder als Varianz s^2 (sprich „sigma Quadrat“) angegeben werden
- hat eine typische Glockenform
Achtung: Der 2Sigmawert ist etwas anderes als die Varianz .
- 2Sigma = s+s
- Varianz = s*s = s hoch 2
Die Form der Glockenkurve, insbesondere das Verhältnis von Höhe und Breite ist abhängig von der Streuung der Werte und vom Maßstab der x- und y-Achse.
- Eine große Streuung bedeutet eine flach ausgezogene Glockenkurve
- Eine geringe Streuung eine schmale steile Kurve
Aus der Glockenkurve lassen sich der arithmetische Mittelwert und die Standardabweichung als Maß für die gerade erwähnte Streuung ablesen.
Das arithmetische Mittel entspricht dem Abszissenabschnitt im Maximum der Kurve
Die Standardabweichung läßt sich aus den Wendepunkten ablesen. (Zur Erinnerung: Wendepunkte einer Kurve sind diejenigen Punkte, in denen die Kurve keine Krümmung hat, wo also die Rechtskrümmung in eine Linkskrümmung übergeht und umgekehrt).
Man kann sich die Bedeutung der Standardabweichung außerdem noch mit Hilfe der folgenden Angabe verdeutlichen, die aus dem Kurvenverlauf ermittelt werden kann. Zwischen m+s und m – sä (1-Sigma-Bereich) liegen 68% aller vorkommenden Werte, zwischen m+2s (obere Warngrenze) und m – 2s(untere Warngrenze) (2-Sigma-Bereich) 95% aller Werte und zwischen m+3s (obere Kontrollgrenze) und m-3s (untere Kontrollgrenze) (3-Sigma-Bereich) liegen 99% aller Werte.
Wenn ich es noch nicht programmiert habe , habe ich es noch nicht verstanden.
Ich habe die Gaussche Normalverteilung in Visual Basic programmiert . Vielleicht wird dann maches klarer . Sie können das Programm als ausführbares Programm herunterladen, brauchen aber vbrun300.dll , um es auszuführen.
gauss.exe vbrun300.dll
Ein Bild vom Programm ( Screenshot )
Zur Programmausführung drücken Sie bitte erst auf den Befehl Normales Koordinatensystem und dann auf den Befehl Gaussche Normalverteilung. Als Mittelwert wird hier willkürlich der Wert E = 3 und als Sigmawert der Wert S = 0,4 angenommen.
Hinter den Befehlsfeld Normales Koordinatensystem liegt folgender Programmtext:
Sub Befehl1_Click ()
- Scale (-10, 10)-(10, -10)‘ Benutzerdefiniertes Koordinatensystem.
- Line (-10, 0)-(10, 0)
- Line (0, -10)-(0, 10)
End Sub
Hinter den Befehlsfeld Gaussche Normalverteilung liegt folgender Programmtext:
Sub Befehl2_Click ()
- Rem E = Erwartungswert von x
- Rem S = Standardabweichung
- E = 3: s = .4: Rem beliebig angenommene Werte für E den Mittelwert der Glocke und S = die Breite der Glocke
- For x = -100 To 100 Step .05
- Rem Formel für die Gausssche Glockenkurve
- y = 1 / (2 * 3.14 * s * s) * E ^ -(x – E) ^ 2 / (2 * s * s)
- PSet (x, y)
- Next x
End Sub
Leider gibt es mit dem Programm Probleme, wenn man den Wert E gleich 0 setzt. Dann steigt das Programm aus.
Zum größeren Verständnis sollte man die lange Formel
y = 1 / (2 * 3.14 * s * s) * E ^ -(x – E) ^ 2 / (2 * s * s)
in Ihre Einzelteile zerlegen und dafür Hilfsvariablen einführen.
k = 1 / (2 * 3.14 * s * s)
h = -(x – E) * (x – E) / (2 * s * s)
y = k * E ^ h
Dann wird die Formel einfacher y = k * E hoch h = k* E ^ h = k * E h
Gründe für die besondere Bedeutung der NVT in der Statistik:
Die NVT ist eine theoretische Verteilung, für die bekannt ist, mit welcher Häufigkeit (Wahrscheinlichkeit) bestimmte Variablenwerte über- oder unterschritten werden bzw. mit welcher Häufigkeit (Wahrscheinlichkeit) Variablenwerte in einem bestimmten Werteintervall liegen.
Viele reale Variablen sind annähernd normalverteilt. Dies gilt insbesondere für natürliche Phänomene wie Temperaturen, Niederschläge, Körpergröße aber auch für einige soziale bzw. gesellschaftliche Variablen, bspw. die Anzahl gemeldeter Pkw auf 1.000 Einwohner. (Auf alle diese Variablen können die für die NVT gewonnenen Erkenntnisse übertragen werden!)
Viele statistische Verfahren basieren auf der Annahme, daß die untersuchten Größen normalverteilt sind.
Hallo!
Ich bin auf der Suche nach einer Formel für die Gaussche Normalverteilung , aber die auf Ihrer Seite ist etwas zu hoch für mich, glaube ich. Könnten Sie mir vielleicht eine Formel erstellen, die X-Werte von 0 bis 1 annimmt und wieder Y Werte von 0-1 zurückgibt? Dabei interessiert mich nicht die ganze Glocke, sondern halt nur eine Seite davon. Dies brauche ich für eine Art Interpolation ( Schätzung ) . Können Sie mir helfen?
Grüße,
Benjamin Wilger
Antwort :
Meine Seite zur Gausverteilung ist nur aus dem Internet aufgesammelt und deswegen didaktisch nicht gut gemacht. Es fehlt zb ein instruktives Bild. Kein Wunder das Sie mit der Seite nicht allzuviel anfangen konnten.
Ich werde versuchen die Seite zu verbessern. ( ist erfolgt )
Testen auf Normalverteilung
Test auf Normalverteilung:
1.Abschätzen:
Teilen Sie ihre Meßwerte in ca 10 gleiche Intervalle auf und betrachten sie die Häufigkeiten in den einzelnen Intervallen.
Die Häufigkeiten sollten schön symmetrisch um einen maximalen Wert herum verteilt sein und sollten einer Gaußschen Glockenkurve ähneln.
2. Aus der Erfahrung heraus sind in meinem Arbeitsgebiet ( der Medizin) viele Meßwerte wie zb Körpergröße, Gewicht, Temperatur , Blutdruck, Puls, Blutzucker und viele weitere Laborwerte nicht normalverteilt.
Man kann sie durch einen Trick normalverteilt machen, wenn man die Einzelwerte logarithmisch transformiert.
3.Viele Statistikprogramme auf dem PC können eingegebene Daten von sich aus auf ihre Normalverteilung testen.
4. Unter http://de.wikipedia.org/wiki/Chi-Quadrat-Anpassungstest ist ein Beispiel für einen Test auf Normalverteilung zu finden.
5. Um das Problem mit der Normalverteilung zu umgehen, kann man mit einem Rangsummentest (Wilcoxon-Test) arbeiten, wenn man zb die Meßwerte aus 2 verschiedenen Gruppen vergleichen will . Dieser Test ist ziemlich einfach zu verstehen, ist verteilungsfrei und liefert doch gut brauchbare statistische Aussagen.
http://home.t-online.de/home/malerczyk/Normalverteilung.html
http://www.itl.nist.gov/div898/handbook/eda/section3/eda3661.htm
http://www.biologie.uni-hamburg.de/b-online/d13/4.htm
http://www.isl.uni-karlsruhe.de/module/statistik/normalverteilung/normalverteilung.html
http://www.bioinf.uni-hannover.de/ausbildung/ol/norm.html
http://www.koopiworld.de/studium/mathe.html
http://www.uni-ulm.de/~cschmid/v2000s/webstat/k1a/k1a_2.htm
Die Geschichte der Normalverteilung
Abraham de Moivre (1667-1754), ein als Hugenotte aus Frankreich vertriebener Mathematiker, der für seinen Lebensunterhalt in London Ratschläge an Glücksspieler erteilte, skizzierte in seiner Schrift „Doctrine of Chances“ (12.11.1733) erstmals den Übergang von der Binomialverteilung zur Normalverteilung.
Carl Friedrich Gauß (1777-1855) arbeitete eine Theorie der Beobachtungsfehler aus, die aufs engste verknüpft ist mit der Normalverteilung, der Streuung und der Methode der kleinsten Quadrate. Seine Erklärung für die Normalkurve: Unzählige Einzeleinflüsse tragen dazu bei, die mehr oder minder großen Abweichungen vom „Durchschnitt“ hervorzurufen, die wir überall beobachten können – und diese Zufallskombination zufälliger Einflüsse unterliegt letztlich den „Gesetzen“ des Glücksspiels, den Regeln der Binomialverteilung mit einer nahezu endlosen Zahl von „Versuchen“.
Adolphe Quételet (1796-1874), belgischer Astronom und Statistiker, Schüler von Jean Baptiste Fourier (1768-1830), errechnete aus der Vielfalt menschlicher Individuen den „homme moyen“ als den von der Natur angestrebten und in unterschiedlichem Maße verfehlten Idealtyp. Bei der Messung des Brustumfangs von 5738 schottischen Soldaten (1844 ?) entdeckte er eine verblüffende Übereinstimmung der beobachteten Werte mit der Normalverteilung (Mittelwert 39.8 Zoll). Quételet hat gezeigt, daß statistische Größen in gewissem Sinne existieren, ohne dafür Erklärungen zu geben – darum bemühte sich:
Sir Francis Galton (1822-1911), Biologe, Kriminologe und Afrikaforscher, befaßte sich unter anderem mit der Verfeinerung von Quételets Vorstellung vom „homme moyen“ und mit der Gesetzmäßigkeit von Zufallsabweichungen. Als einer der ersten führte er quantitative Methoden in die Biologie ein, wobei er unter anderem Meßskalen für alle nur erdenklichen Körpermerkmale entwarf – sogar für die weibliche Schönheit. Er schrieb: „Ich kenne kaum etwas, das unsere Phantasie so mitreißen kann wie die wundervolle Form kosmischer Ordnung, die das ‚Gesetz der Fehlerhäufigkeit‘ ausdrückt. Hätten die Griechen es gekannt, sie hätten es personifiziert und als Gottheit angebetet. In der wildesten Konfusion verbreitet es harmonische Ruh; je ärger die Anarchie, um so souveräner ist seine Herrschaft. Hinter dem Schleier des Chaos tritt es als unerhoffte und wunderschöne Form der Regelmäßigkeit hervor.“
Clerk Maxwell (1831-1879) übernahm Quételets Normalverteilung als Verteilung der Geschwindigkeit von Gasmolekülen. Er hatte eine Buchbesprechung von Herschel über Quételet gelesen, in der über die Geschwindigkeit von Gasmolekülen spekuliert wurde.
Karl Pearson (1857-1936), der Vater der modernen mathematischen Statistik, stellte fest, daß es in der Natur durchaus auch nicht-normal verteilte Größen gab, fand jedoch, daß so manche sich als eine Verflechtung von zwei und mehr Normalverteilungen entpuppte.
Alexander Michailowitsch Ljapunow (1857-1918) bewies 1901 erstmalig den zentralen Grenzwertsatz: Die Summe von genügend vielen unabhängigen Zufallsgrößen ist näherungsweise normalverteilt, wie immer auch jede einzelne dieser Zufallsgrößen verteilt sein mag. Dieser Satz erklärt das häufige Auftreten der Normalverteilung in der Natur; denn viele Größen (Körpergröße, Gewicht, …) werden durch die Überlagerung vieler unabhängiger Einflüsse (Zufallsgrößen) bestimmt.
Hinweis: Die ursprüngliche Seite madeasy.de existiert leider nicht mehr. Deshalb haben wir hier einige der wichtigsten Inhalte per Internet Archive (Wayback Machine) wieder hergestellt, um Sie für die Nachwelt zu erhalten.[/su_note]