Logarithmen

Einleitung

Mit dem Logarithmus kann man sehr große Zahlen übersichtlich und klein machen.

Aus 1 000 000 wird beispielsweise 10^6 ( Sprich 10 hoch 6 = 10 * 10 * 10 * 10 *10 *10)

Dabei ist die Hochzahl 6     der Logarithmus von 1 000 000 zur hier gewählten Basiszahl 10 .

Der Begriff Hochzahl und Exponent sind identisch .

Die Logarithmusfunktion y = log_b (x)  liefert für jede beliebige positive Zahl x einen Wert.

So ist der Logarithmus der Zahl 1 234 567 zur Basis 10 gleich log₁₀ (1234567) = 6.09151466408626

Insbesondere für Werte, die sehr klein oder sehr groß sind oder die einen sehr großen Wertebereich einnehmen können, haben sich Logarithmen sehr bewährt.

Da die Logarithmusfunktion mit größer werden x Werten stetig wächst , bleiben logische Zusammenhänge, die für den x Wert gelten meist auch für den Logarithmus von x erhalten.

Anwendung von Logarithmen

• pH = Säurewert von chemischen Lösungen
• dB = Dezibel = Messung der Lautstärke
• bit = Informationseinheit = Messung der Informationsmenge
• zbit = Entropieeinheit  = Maßzahl der Entropie = Menge an Zufall
• Logarithmuspapier in der Statistik

Abkürzungen

• exp Exponentialfunktion
• ln  = log_e Natürlicher Logarithmus zur Basis e
• lg  = log₁₀ Logarithmus zur Basis 10
• lb  oder ld = log₂  Logarithmus zur Basis 2, binärer Logarithmus , dualer Logarithmus
• log_b allgemeiner Logarithmus mit der beliebigen Basis b

Definition

log_ba ist eine eindeutig bestimmte Zahl y , mit der man b potenzieren muß , um x zu erhalten .

y = log_bx  <=>  b^y = x        oder b^y =x

Beispiel :

• log₁₀100 = 2 , denn 10² = 100
• log₂8 = 3 , denn 2³ = 8

Beachte

• Der Logarithmus ist für 0 und negative Zahlen nicht definiert !
• dh. x kann nur eine positive Zahl > 0 sein ,  wenn  y = log x
• y kann von – Unendlich bis + Unendlich reichen
• beim Programmieren mit Basic gibt es nur eine festgelegte Basis e
• zur Vermeidung von tiefgestellten Zeichen wird die Zahl, die logarithmiert werden soll,  in Klammern gesetzt.
• Beispiel Programm:
• for x = 1 to 10
  • y = log (x)
  • print y
• next x

Rechenregeln, Logarithmengesetze

log_b ( u * v ) = log_b u + log_b v

Beispiel:

• log₁₀ ( 10 * 100 ) = log₁₀ 10 + log₁₀ 100 = 1 + 2 = 3

log_b ( u / v ) = log_b u – log_b v

Beispiel:

• log₁₀ ( 100 / 10 ) = log₁₀ 100 – log₁₀ 10 = 2 – 1 = 1

log_b (u^z) = z * log_b u

Beispiel:

• log₁₀ 100² = 2 * log₁₀ 100 = 2 * 2 = 4

log_b (u^1/z) =   log_b ^(z Ö u) = 1 /z * log_b u

Beispiel:

• log₁₀ ²Ö100 = 1/2 * log₁₀ 100 = 1/2 * 2 = 1

log_a1 = 0

Beispiel:

• log₁₀ 1 = 0        log₂ 1 = 0        log_e 1 = 0

log_a a = 1

Beispiel:

• log₁₀ 10 = 1        log₂ 2 = 1        log_e e = e

log_a (1/x) = – log_a (x)

Beispiel:

• log₁₀ (1/100) =- log₁₀ (100) = – 2
• log₂ (1/8) =- log₂ (8) = – 3

Basisumrechnung

log_ca = log_ba / log_bc

Beispiel : log₁₀8 = log₂8 / log₂10  =  ca. 3 / 3,32 = ca. 0,90

Bilder

Abbildung: Funktion y = log₂ x

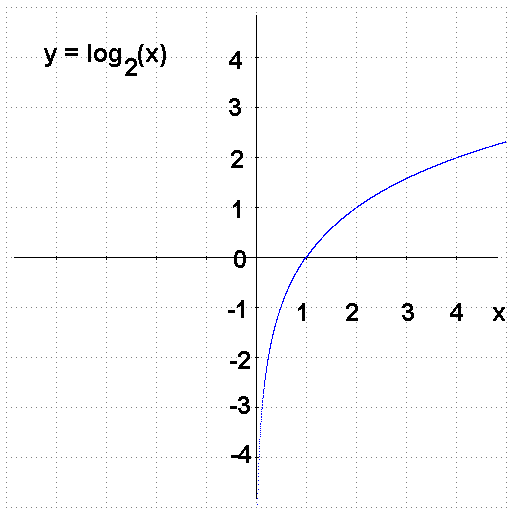
Abbildung der Exponentialfunktion y = 2^x = 2^x

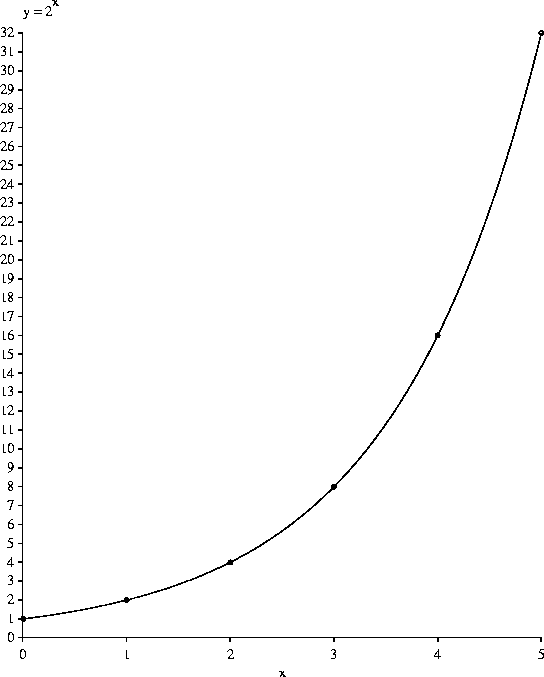
Logarithmusfunktion y = log₂x

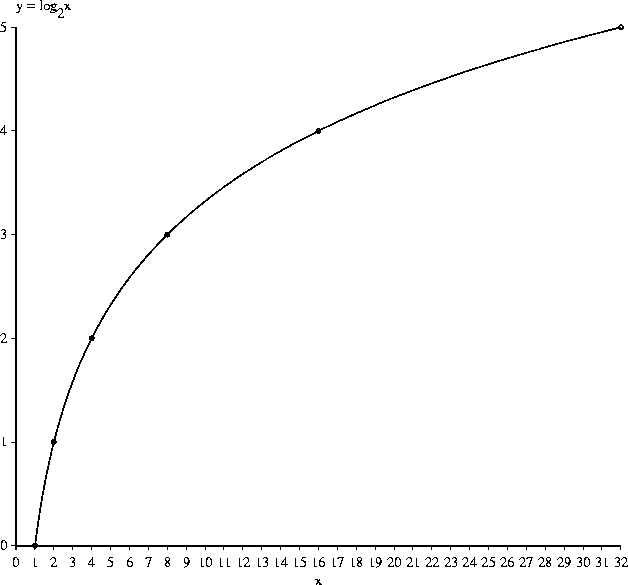
Links

Logarithmusrechner mit Quelltext

http://www.fh-kaernten.ac.at/%7Epester/scripts/Logarithmus1.htm

http://iva.uni-ulm.de/physik/REPETITORIUM/MATHEMATIK/2/02.html